Table of Contents
“How will you calculate complexity of algorithm” is very common question in interview.How will you compare two algorithm? How running time get affected when input size is quite large? So these are some question which is frequently asked in interview.In this post,We will have basic introduction on complexity of algorithm and also to big o notation
What is an algorithm?
Why do you need to evaluate an algorithm?
Counting number of instructions:
|
1 2 3 4 5 6 7 8 9 |
int n=array.length for (int i = 0; i < n; i++) { if(array[i]==elementToBeSearched) return true; } return false; |
- For assigning a value to a variable
- For comparting two values
- Multiply or addition
- Return statement
In Worst case:
So :
|
1 2 3 4 5 |
if(array[i]==elementToBeSearched) ,i++ and i<n <b>will be executed n times</b> int n=array.length,i=0,return true or false <strong>will be executed one time. </strong> |
Asymptotic behaviour :
- As n grows larger, we can ignore constant 3 as it will be always 3 irrespective of value of n. It makes sense as you can consider 3 as initialization constant and different language may take different time for initialization.So other function remains f(n)=3n.
- We can ignore constant multiplier as different programming language may compile the code differently. For example array look up may take different number of instructions in different languages. So what we are left with is f(n)=n
How will you compare algorithms?
f(n) =4n^2 +2n+4 and f(n) =4n+4
so here
f(1)=4+2+4
f(2)=16+4+4
f(3)=36+6+4
f(4)=64+8+4
….
As you can see here contribution of n^22 increasing with increasing value of n.So for very large value of n,contribution of n^2 will be 99% of value on f(n).So here we can ignore low order terms as they are relatively insignificant as described above.In this f(n),we can ignore 2n and 4.so
n^2+2n+4 ——–>n^2
so here
f(1)=4+4
f(2)=8+4
f(3)=12+4
f(4)=16+4
….
As you can see here contribution of n increasing with increasing value of n.So for very large value of n,contribution of n will be 99% of value on f(n).So here we can ignore low order terms as they are relatively insignificant.In this f(n),we can ignore 4 and also 4 as constant multiplier as seen above so
4n+4 ——–>nSo here n is highest rate of growth.
Point to be noted :
We are dropping all the terms which are growing slowly and keep one which grows fastest.
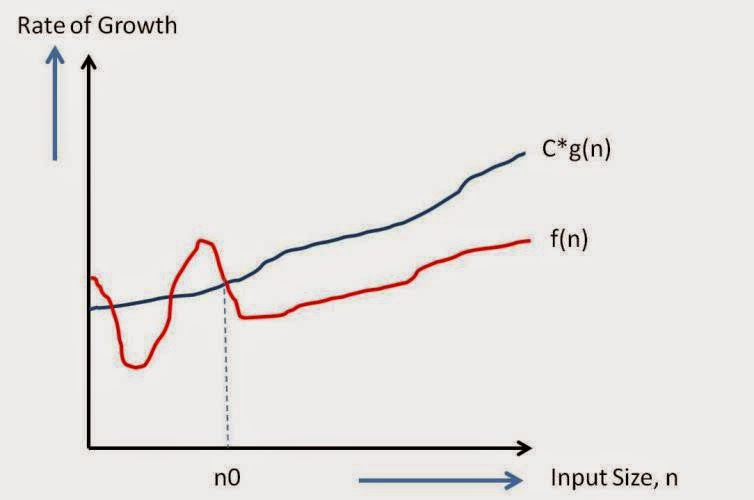
Big O Notation:
So O(g(n)) is a good way to show complexity of algorithm.
Lets take some example and calculate value for c and n0.
1. f(n)=4n+3
Writing in a form of f(n)<=c*g(n) with f(n)=4n+3 and g(n)=5n
4n+3<=5n for n0=3 and c=5.
or 4n+3<=6n for n0=2 and c=6
Writing in a form of f(n)<=c*g(n) with f(n)=4n+3 and g(n)=6n
so there can be multiple values for n0 and c for which f(n)<=c g(n) will get satisfied.
2. f(n)=4n^2+2n+4
Writing in a form of f(n)<=c*g(n) with f(n)=4n^2 +2n+4 and g(n)=5n^2
4n^2 +2n+4<=5n^2 for n0=4 and c=5
Rules of thumb for calculating complexity of algorithm:
Consecutive statements:
|
1 2 3 4 |
int m=0; // executed in constant time c1 m=m+1; // executed in constant time c2 |
So O(f(n))=1
Calculating complexity of a simple loop:
Time complexity of a loop can be determined by running time of statements inside loop multiplied by total number of iterations.
|
1 2 3 4 5 6 7 |
int m=0; // executed in constant time c1 // executed n times for (int i = 0; i < n; i++) { m=m+1; // executed in constant time c2 } |
f(n)=c2*n+c1;
So O(n)=n
It is product of iterations of each loop.
|
1 2 3 4 5 6 7 8 9 10 11 |
int m=0; executed in constant time c1 // Outer loop will be executed n times for (int i = 0; i < n; i++) { // Inner loop will be executed n times for(int j = 0; j < n; j++) { m=m+1; executed in constant time c2 } } |
f(n)=c2*n*n + c1
So O(f(n))=n^2
When you have if and else statement, then time complexity is calculated with whichever of them is larger.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
int countOfEven=0;//executed in constant time c1 int countOfOdd=0; //executed in constant time c2 int k=0; //executed in constant time c3 //loop will be executed n times for (int i = 0; i < n; i++) { if(i%2==0) //executed in constant time c4 { countOfEven++; //executed in constant time c5 k=k+1; //executed in constant time c6 } else countOfOdd++; //executed in constant time c7 } |
f(n)=c1+c2+c3+(c4+c5+c6)*n
So o(f(n))=n
Logarithmic complexity
Lets understand logarithmic complexity with the help of example.You might know about binary search.When you want to find a value in sorted array, we use binary search.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
public int binarySearch(int[] sorted, int first, int last, int elementToBeSearched) { int iteration=0; while (first < last) { iteration++; System.out.println("i"+iteration); int mid = (first + last) / 2; // Compute mid point. System.out.println(mid); if (elementToBeSearched < sorted[mid]) { last = mid; // repeat search in first half. } else if (elementToBeSearched > sorted[mid]) { first = mid + 1; // Repeat search in last half. } else { return mid; // Found it. return position } } return -1; // Failed to find element } |
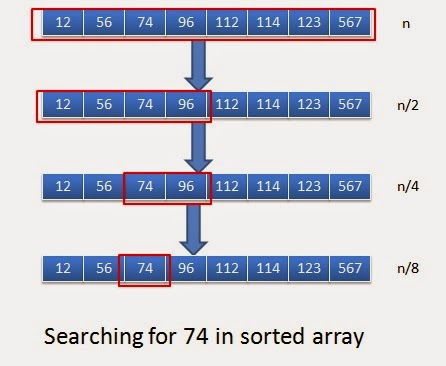
Now let’s assume our soreted array is:
|
1 2 3 |
int[] sortedArray={12,56,74,96,112,114,123,567}; |
and we want to search for 74 in above array. Below diagram will explain how binary search will work here.
When you observe closely, in each of the iteration you are cutting scope of array to the half. In every iteration, we are overriding value of first or last depending on soretedArray[mid].
So for
0th iteration : n
1th iteration: n/2
2nd iteration n/4
3rd iteration n/8.
Generalizing above equation:
For ith iteration : n/2i
So iteration will end , when we have 1 element left i.e. for any i, which will be our last iteration:
1=n/2i;
2i=n;
after taking log
i= log(n);
so it concludes that number of iteration requires to do binary search is log(n) so complexity of binary search is log(n)
It makes sense as in our example, we have n as 8 . It took 3 iterations(8->4->2->1) and 3 is log(8).
So If we are dividing input size by k in each iteration,then its complexity will be O(logk(n)) that is log(n) base k.
Lets take an example:
|
1 2 3 4 5 6 7 |
int m=0; // executed log(n) times for (int i = 0; i < n; i=i*2) { m=m+1; } |
Complexity of above code will be O(log(n)).
Exercise:
Lets do some exercise and find complexity of given code:
1.
|
1 2 3 4 5 6 |
int m=0; for (int i = 0; i < n; i++) { m=m+1; } |
Ans:
|
1 2 3 4 5 6 7 |
int m=0; // Executed n times for (int i = 0; i < n; i++) { m=m+1; } |
Complexity will be O(n)
2.
|
1 2 3 4 5 6 7 8 9 10 11 |
int m=0; for (int i = 0; i < n; i++) { m=m+1; } for (int i = 0; i < n; i++) { for(int j = 0; j < n; j++) m=m+1; } } |
Ans:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
int m=0; // Executed n times for (int i = 0; i < n; i++) { m=m+1; } // outer loop executed n times for (int i = 0; i < n; i++) { // inner loop executed n times for(int j = 0; j < n; j++) m=m+1; } |
|
1 2 3 |
} |
Complexity will be :n+n*n —>O(n^2)
3.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
int m=0; // outer loop executed n times for (int i = 0; i < n; i++) { // middle loop executed n/2 times for(int j = n/2; j < n; j++) for(int k=0;k*k < n; k++ ) m=m+1; } } } |
Ans:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
int m=0; // outer loop executed n times for (int i = 0; i < n; i++) { // middle loop executed n/2 times for(int j = n/2; j < n; j++) // inner loop executed log(n) times for(int k=0;k*k < n; k++ ) m=m+1; } } } |
Complexity will be n*n/2*log(n)–> n^2log(n)
4.
|
1 2 3 4 5 6 7 8 9 10 |
int m=0; for (int i = n/2; i < n; i++) { for(int j = n/2; j < n; j++) for(int k=0;k < n; k++ ) m=m+1; } |
Ans:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
int m=0; // outer loop executed n/2 times for (int i = n/2; i < n; i++) { // middle loop executed n/2 times for(int j = n/2; j < n; j++) // inner loop executed n times for(int k=0;k < n; k++ ) m=m+1; } |
Complexity will be n/2*n/2*n –> n^3



superb explanation.I went through many explanations to understand time complex before this.But couldnt understand.thankyou soo much for this explanation