If you want to practice data structure and algorithm programs, you can go through 100+ java coding interview questions.
In this post, we will see how to find lowest common ancestor(LCA) of two nodes in binary search tree.
We have already seen how to find LCA in binary tree. It is much simple than that.
Lets understand with example.
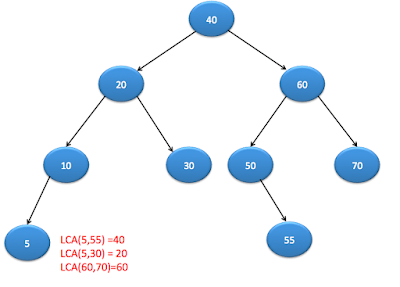
As you can see here, LCA is nothing but lowest common parent of two nodes.
Recursive Algorithm (For nodes A and B):
- If node is null, return it
- If node is greater than A and B, traverse left subtree
- If node is lesser than A and B , traverse right subtree.
- If above both condition do not satisfy, then node is LCA of A and B
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
public static TreeNode lowestCommonAncestorForBinarySearchTree(TreeNode root, TreeNode a, TreeNode b) { if(root==null) return null;; if(root.data>a.data && root.data > b.data) { return lowestCommonAncestorForBinarySearchTree(root.left,a,b); } else if(root.data < a.data && root.data < b.data) { return lowestCommonAncestorForBinarySearchTree(root.right,a,b); } // if you reach at this place, then it is LCA for given two nodes because a and b are on either side of root. return root; } |
Iterative solution:
It is similar to recursive solution, here we are using while loop to traverse nodes.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
public static TreeNode LCAItr(TreeNode root, TreeNode a, TreeNode b) { while(root!=null) { if(root.data>a.data && root.data > b.data) { root=root.left; } else if(root.data < a.data && root.data < b.data) { root=root.right; } else { return root; } } return root; } |
Complete java program:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 |
package org.arpit.java2blog; public class BinaryTree { public static class TreeNode { int data; TreeNode left; TreeNode right; TreeNode(int data) { this.data=data; } } public static TreeNode lowestCommonAncestorForBinarySearchTree(TreeNode root, TreeNode a, TreeNode b) { if(root==null) return null;; if(root.data>a.data && root.data > b.data) { return lowestCommonAncestorForBinarySearchTree(root.left,a,b); } else if(root.data < a.data && root.data < b.data) { return lowestCommonAncestorForBinarySearchTree(root.right,a,b); } // if you reach at this place, then it is LCA for given two nodes because a and b are on either side of root. return root; } public static TreeNode LCAItr(TreeNode root, TreeNode a, TreeNode b) { while(root!=null) { if(root.data>a.data && root.data > b.data) { root=root.left; } else if(root.data < a.data && root.data < b.data) { root=root.right; } else { return root; } } return root; } public static void main(String[] args) { BinaryTree bi=new BinaryTree(); // Creating a binary tree TreeNode rootNode=createBinaryTree(); System.out.println("Lowest common ancestor for node 5 and 30 using Recursion:"); TreeNode node5=new TreeNode(5); TreeNode node30=new TreeNode(30); System.out.println(lowestCommonAncestorForBinarySearchTree(rootNode,node5,node30).data); System.out.println("Lowest common ancestor for node 5 and 30 using Iteration:"); System.out.println(LCAItr(rootNode,node5,node30).data); } public static TreeNode createBinaryTree() { TreeNode rootNode =new TreeNode(40); TreeNode node20=new TreeNode(20); TreeNode node10=new TreeNode(10); TreeNode node30=new TreeNode(30); TreeNode node60=new TreeNode(60); TreeNode node50=new TreeNode(50); TreeNode node70=new TreeNode(70); TreeNode node5=new TreeNode(5); TreeNode node45=new TreeNode(45); TreeNode node55=new TreeNode(55); rootNode.left=node20; rootNode.right=node60; node20.left=node10; node20.right=node30; node60.left=node50; node60.right=node70; node10.left=node5; node50.right=node55; return rootNode; } } |
|
1 2 3 4 5 6 |
Lowest common ancestor for node 5 and 30 using Recursion: 20 Lowest common ancestor for node 5 and 30 using Iteration: 20 |
Was this post helpful?
Let us know if this post was helpful. Feedbacks are monitored on daily basis. Please do provide feedback as that\'s the only way to improve.


