Table of Contents
If you want to practice data structure and algorithm programs, you can go through 100+ java coding interview questions.
In this post, we will see how to delete a node from binary search tree.
There are two parts to it.
- Search the node
- After searching that node, delete the node.
There are three cases which we may need to consider while deleting a node from binary search tree.
- If node has
no child - If node has
one child - If node has
two children.
If node has no child
It is pretty straight forward case. We need to search the node and make it null.
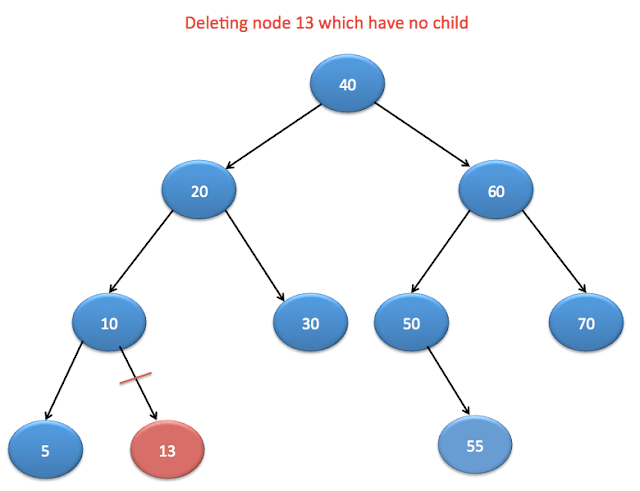

If node has one children
If node have one children then we need to connect parent of removed node directly to child of the removed node.
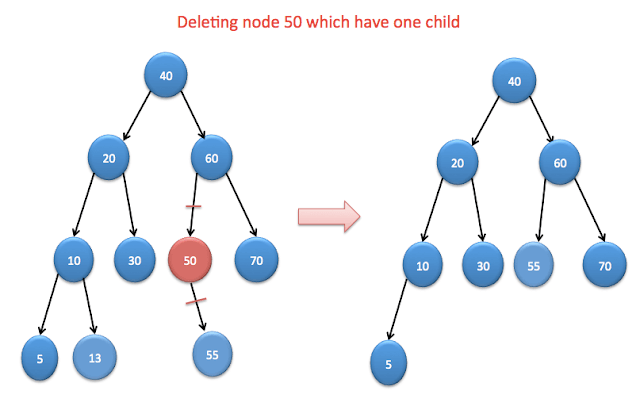

If node has two children
It is complicated case. If it has two nodes, we need to connect parent of node to the leftmost node(minimum) of right sub tree or rightmost node(maximum) of left subtree.
Lets understand this case with example:
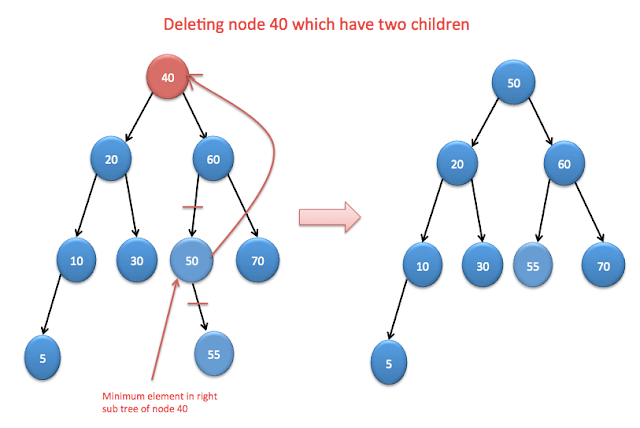
As you can see, we are replacing node 40 with node 50. Node 50 is minimum element in right subtree of 40 and deleting node 50 after moving as there will duplicate nodes.
Why minimum element of right sub tree?
Here we are using binary search tree property that tree can be represented in multiple ways.
For example:
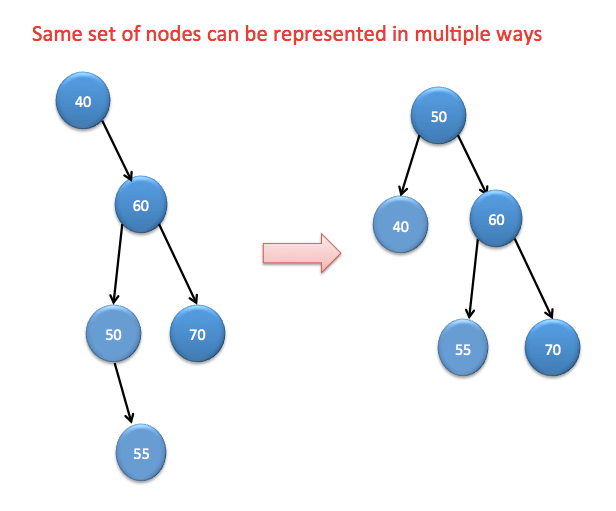
When you run above program, you will get following output:

We are using same property while deleting nodes with two children.
Java program to delete node in Binary search tree
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 |
package org.arpit.java2blog.binarysearchtree; public class BinarySearchTreeDeleteMain { public static class TreeNode { int data; TreeNode left; TreeNode right; TreeNode(int data) { this.data = data; } } // Get minimum element in binary search tree public static TreeNode minimumElement(TreeNode root) { if (root.left == null) return root; else { return minimumElement(root.left); } } public static TreeNode deleteNode(TreeNode root, int value) { if (root == null) return null; if (root.data > value) { root.left = deleteNode(root.left, value); } else if (root.data < value) { root.right = deleteNode(root.right, value); } else { // if nodeToBeDeleted have both children if (root.left != null && root.right != null) { TreeNode temp = root; // Finding minimum element from right TreeNode minNodeForRight = minimumElement(temp.right); // Replacing current node with minimum node from right subtree root.data = minNodeForRight.data; // Deleting minimum node from right now root.right = deleteNode(root.right, minNodeForRight.data); } // if nodeToBeDeleted has only left child else if (root.left != null) { root = root.left; } // if nodeToBeDeleted has only right child else if (root.right != null) { root = root.right; } // if nodeToBeDeleted do not have child (Leaf node) else root = null; } return root; } public static TreeNode insert(TreeNode root, TreeNode nodeToBeInserted) { if (root == null) { root = nodeToBeInserted; return root; } if (root.data > nodeToBeInserted.data) { if (root.left == null) root.left = nodeToBeInserted; else insert(root.left, nodeToBeInserted); } else if (root.data < nodeToBeInserted.data) if (root.right == null) root.right = nodeToBeInserted; else insert(root.right, nodeToBeInserted); return root; } public static void inOrder(TreeNode root) { if (root == null) return; inOrder(root.left); System.out.print(root.data + " "); inOrder(root.right); } public static void main(String[] args) { // Creating a binary search tree TreeNode rootNode = createBinarySearchTree(); System.out.println("Binary tree:"); inOrder(rootNode); System.out.println(); System.out.println("Deleting node 40 which have two children:"); TreeNode rootNodeRes = deleteNode(rootNode, 40); inOrder(rootNodeRes); } public static TreeNode createBinarySearchTree() { TreeNode rootNode = new TreeNode(40); TreeNode node20 = new TreeNode(20); TreeNode node10 = new TreeNode(10); TreeNode node30 = new TreeNode(30); TreeNode node60 = new TreeNode(60); TreeNode node50 = new TreeNode(50); TreeNode node70 = new TreeNode(70); TreeNode node5 = new TreeNode(5); TreeNode node13 = new TreeNode(13); TreeNode node55 = new TreeNode(55); insert(null, rootNode); insert(rootNode, node20); insert(rootNode, node10); insert(rootNode, node30); insert(rootNode, node60); insert(rootNode, node50); insert(rootNode, node70); insert(rootNode, node5); insert(rootNode, node13); insert(rootNode, node55); return rootNode; } } |
|
1 2 3 4 5 6 |
Binary tree: 5 10 13 20 30 40 50 55 60 70 Deleting node 40 which have two children: 5 10 13 20 30 50 55 60 70 |
Was this post helpful?
Let us know if this post was helpful. Feedbacks are monitored on daily basis. Please do provide feedback as that\'s the only way to improve.



Thank you very much Arpit, very nice, clean and understandable code for newbies!
Thank you very much for nice explanation.
There is a small correction to deletion code.
// Deleting minimum node from right now
deleteNode(root.right, minNodeForRight.data);
The above statement should be assigned to root.right, else the duplicate node won’t be removed.
Thanks,
Kasi