If you want to practice data structure and algorithm programs, you can go through 100+ java coding interview questions.
Table of Contents
Graph traversal Algorithms:
Breadth first search is graph traversal algorithm. In this algorithm, lets say we start with node i, then we will visit neighbours of i, then neighbours of neighbours of i and so on.
Algorithm:
Steps for Breadth first search:
- Create empty queue and push root node to it.
- Do the following when queue is not empty
- Pop a node from queue and print it.
- Find neighbours of node with the help of adjacency matrix and check if node is already visited or not.
- Push neighbours of node into queue if not null
Lets understand with the help of example:
Lets say graph is:
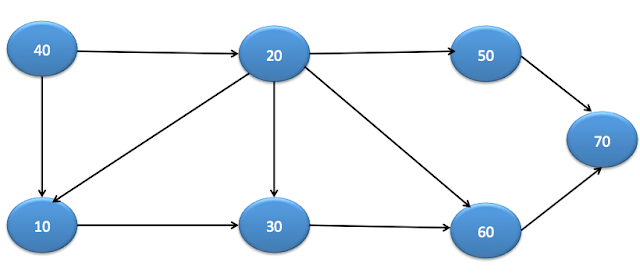
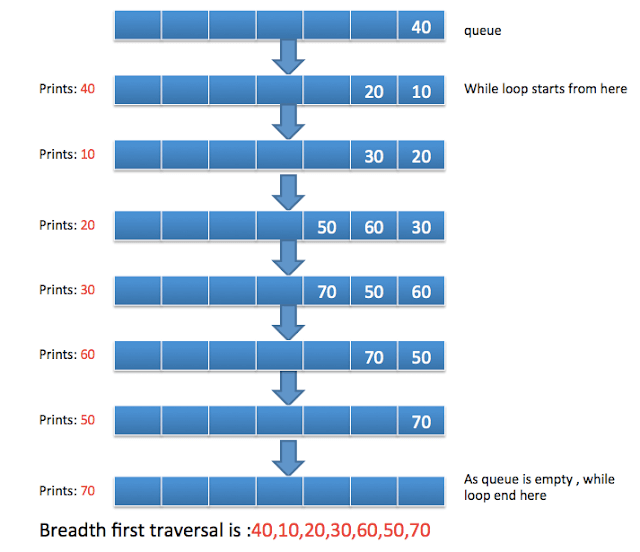
Java BFS Example
There are two ways to represent a graph.
- Using Neighbours list
- Using Adjacency Matrix
Using Neighbours list
In this, you can have List<Node> as neighbours in Node class as below.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
package org.arpit.java2blog.graph; import java.util.ArrayList; import java.util.LinkedList; import java.util.List; import java.util.Queue; public class BreadthFirstSearchExampleNeighbourList { private Queue<Node> queue; static ArrayList<Node> nodes=new ArrayList<Node>(); static class Node { int data; boolean visited; List<Node> neighbours; Node(int data) { this.data=data; this.neighbours=new ArrayList<>(); } public void addneighbours(Node neighbourNode) { this.neighbours.add(neighbourNode); } public List<Node> getNeighbours() { return neighbours; } public void setNeighbours(List<Node> neighbours) { this.neighbours = neighbours; } } public BreadthFirstSearchExampleNeighbourList() { queue = new LinkedList<Node>(); } public void bfs(Node node) { queue.add(node); node.visited=true; while (!queue.isEmpty()) { Node element=queue.remove(); System.out.print(element.data + "t"); List<Node> neighbours=element.getNeighbours(); for (int i = 0; i < neighbours.size(); i++) { Node n=neighbours.get(i); if(n!=null && !n.visited) { queue.add(n); n.visited=true; } } } } public static void main(String arg[]) { Node node40 =new Node(40); Node node10 =new Node(10); Node node20 =new Node(20); Node node30 =new Node(30); Node node60 =new Node(60); Node node50 =new Node(50); Node node70 =new Node(70); node40.addneighbours(node10); node40.addneighbours(node20); node10.addneighbours(node30); node20.addneighbours(node10); node20.addneighbours(node30); node20.addneighbours(node60); node20.addneighbours(node50); node30.addneighbours(node60); node60.addneighbours(node70); node50.addneighbours(node70); System.out.println("The BFS traversal of the graph is "); BreadthFirstSearchExampleNeighbourList bfsExample = new BreadthFirstSearchExampleNeighbourList(); bfsExample.bfs(node40); } } |
When you run above program, you will get below output:
40 10 20 30 60 50 70
Using Adjacency Matrix
Adjacency_matrix is used to find the connection between two nodes.
if adjacency_matrix[i][j]==1, then nodes at index i and index j are connected
Below diagram will help you to understand adjacency matrix.

Create BreadthFirstSearchExample.java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 |
package org.arpit.java2blog.graph; import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; public class BreadthFirstSearchExample { private Queue<Node> queue; static ArrayList<Node> nodes=new ArrayList<Node>(); static class Node { int data; boolean visited; Node(int data) { this.data=data; } } public BreadthFirstSearchExample() { queue = new LinkedList<Node>(); } // find neighbors of node using adjacency matrix // if adjacency_matrix[i][j]==1, then nodes at index i and index j are connected public ArrayList<Node> findNeighbours(int adjacency_matrix[][],Node x) { int nodeIndex=-1; ArrayList<Node> neighbours=new ArrayList<Node>(); for (int i = 0; i < nodes.size(); i++) { if(nodes.get(i).equals(x)) { nodeIndex=i; break; } } if(nodeIndex!=-1) { for (int j = 0; j < adjacency_matrix[nodeIndex].length; j++) { if(adjacency_matrix[nodeIndex][j]==1) { neighbours.add(nodes.get(j)); } } } return neighbours; } public void bfs(int adjacency_matrix[][], Node node) { queue.add(node); node.visited=true; while (!queue.isEmpty()) { Node element=queue.remove(); System.out.print(element.data + "t"); ArrayList<Node> neighbours=findNeighbours(adjacency_matrix,element); for (int i = 0; i < neighbours.size(); i++) { Node n=neighbours.get(i); if(n!=null && !n.visited) { queue.add(n); n.visited=true; } } } } public static void main(String arg[]) { Node node40 =new Node(40); Node node10 =new Node(10); Node node20 =new Node(20); Node node30 =new Node(30); Node node60 =new Node(60); Node node50 =new Node(50); Node node70 =new Node(70); nodes.add(node40); nodes.add(node10); nodes.add(node20); nodes.add(node30); nodes.add(node60); nodes.add(node50); nodes.add(node70); int adjacency_matrix[][] = { {0,1,1,0,0,0,0}, // Node 1: 40 {0,0,0,1,0,0,0}, // Node 2 :10 {0,1,0,1,1,1,0}, // Node 3: 20 {0,0,0,0,1,0,0}, // Node 4: 30 {0,0,0,0,0,0,1}, // Node 5: 60 {0,0,0,0,0,0,1}, // Node 6: 50 {0,0,0,0,0,0,0}, // Node 7: 70 }; System.out.println("The BFS traversal of the graph is "); BreadthFirstSearchExample bfsExample = new BreadthFirstSearchExample(); bfsExample.bfs(adjacency_matrix, node40); } } |
When you run above program, you will get below output:
|
1 2 3 4 |
The BFS traversal of the graph is 40 10 20 30 60 50 70 |
Please go through Algorithm Interview Programs in java for more such programs.


